Safe, Optimal, Real-time Trajectory Planning with a Parallel Constrained Bernstein Algorithm

To move through the world, mobile robots typically use a receding-horizon strategy, wherein they execute an old plan while computing a new plan to incorporate new sensor information. A plan should be dynamically feasible, meaning it obeys constraints like the robot’s dynamics and obstacle avoidance; it should have liveness, meaning the robot does not stop to plan so frequently that it cannot accomplish tasks; and it should be optimal, meaning that the robot tries to satisfy a user-specified cost function such as reaching a goal location as quickly as possible. Reachability-based Trajectory Design (RTD) is a planning method that can generate provably dynamically-feasible plans. However, RTD solves a nonlinear polynmial optimization program at each planning iteration, preventing optimality guarantees; furthermore, RTD can struggle with liveness because the robot must brake to a stop when the solver finds local minima or cannot find a feasible solution. This paper proposes RTD*, which certifiably finds the globally optimal plan (if such a plan exists) at each planning iteration. This method is enabled by a novel Parallelized Constrained Bernstein Algorithm (PCBA), which is a branch-and-bound method for polynomial optimization. The contributions of this paper are:

1. the implementation of PCBA;

2. proofs of bounds on the time and memory usage of PCBA;

3. a comparison of PCBA to state of the art solvers; and the demonstration of PCBA/RTD* on a mobile robot.

RTD* outperforms RTD in terms of optimality and liveness for real-time planning in a variety of environments with randomly-placed obstacles.

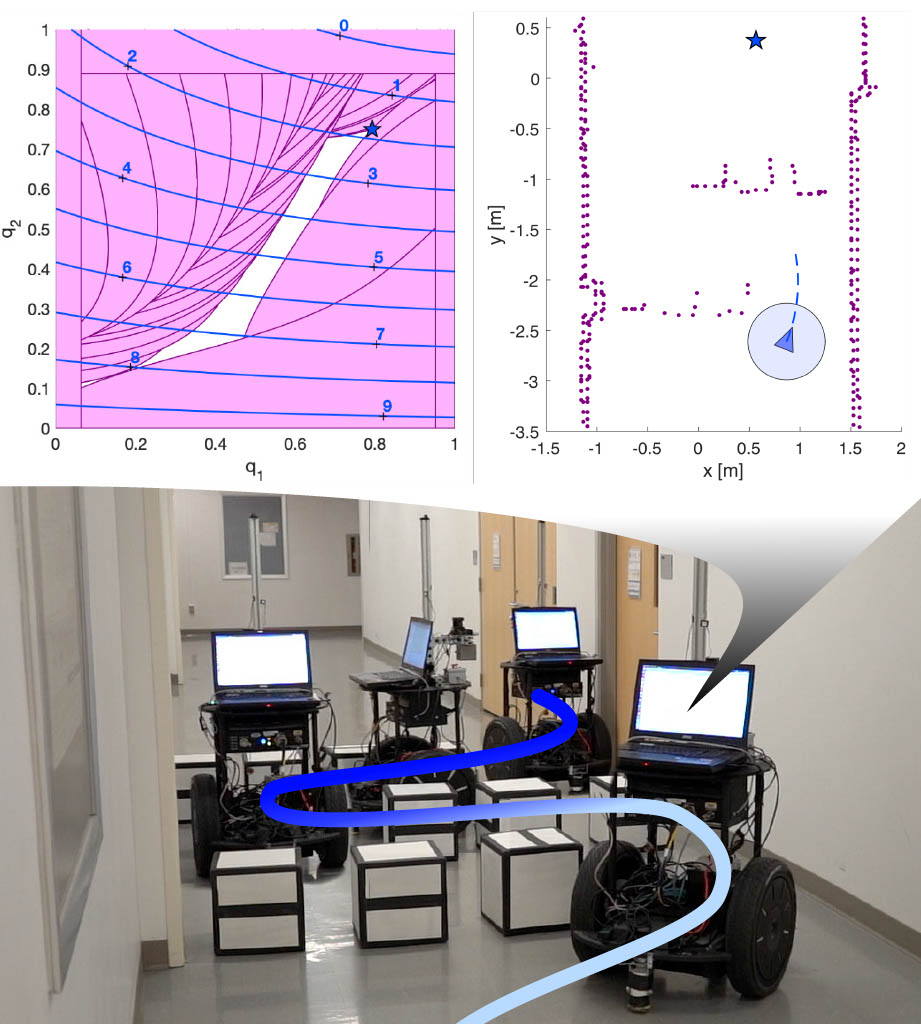
A Segway RMP mobile robot using the proposed PCBA/RTD* method to autonomously navigate a tight obstacle blockade. The executed trajectory is shown fading from light to dark blue as time passes, and the robot is shown at four different time instances. The top right plot shows the Segway’s (blue circle with triangle indicating heading) view of the world at one planning iteration, with obstacles detected by a planar lidar (purple points). The top left plot shows the optimization program solved at the same planning iteration; the decision variable is (q1, q2), which parameterizes the velocity and yaw rate of a trajectory plan; the pink regions are infeasible with respect to constraints generated by the obstacle points in the right plot; and the blue contours with number labels depict the cost function, which is constructed to encourage the Segway to reach a waypoint (the star in the top right plot). The optimal solution found by PCBA is shown as a star on the left plot, in the non-convex feasible area (white). This optimal solution generates a provably-safe trajectory for the Segway to track, shown as a blue dashed line in the right plot.

Hardware demonstration video: https://www.youtube.com/watch?v=YcH4WAzqPFY

For citation, please refer to

(Zhang et al., 2020)